Tunizija! Djerba! (Kje je to?) Egipt! Turčija! nas vabi s panoja potovalne agencije adriatica.net zraven Konzorcija v Ljubljani. (Reklama za storjeno škodo.) Ampak koliko to stane! (Končen znesek seveda ni napisan.) In koliko časa gre za obisk enega ubogega koščka sveta! (Ja, nimam česa dodati.)

Lahko potujemo bistveno veličastneje in bistveno ceneje. Če predpostavimo, da smo svobodni, se lahko pustimo mučiti in odpeljati nekam, kjer se nam bo ves čas kolcalo po domu, po domači postelji, po domači kopalnici, in če gremo v ZDA, potem obvezno še po naših špecerijah itd. itd. Lahko pa gremo s prstom po zemljevidu tako kot, vendar ne čisto tako kot v osnovni šoli.

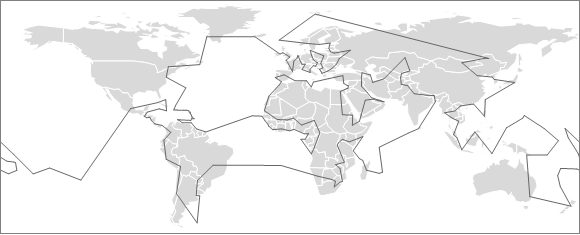
Iz Ljubljane do San Marina in naprej do Rima, Vatikana, Monaka in tako prek vseh svetovnih prestolnic okrog sveta, nakar se prek Dunaja, Bratislave in Zagreba vrnemo domov. (Klik za večjo, 1500 pikslov razsežno sliko.) Potujemo vzdolž lokov velikih krogov, ki predstavljajo najkrajše poti med pari točk na krogli. Obiščemo 237 držav in toliko glavnih mest in naredimo okoli 178 000 km, kar je za štiri cele kroge po ekvatorju pa še nekaj. A to je najkrajša pot, na kateri obiščemo vse prestolnice in se vrnemo domov.

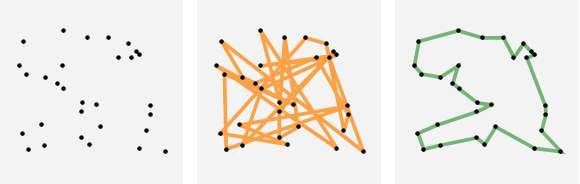
Kako stopiti nanjo, kako poiskati to najkrajšo pot, si poglejmo ob dveh enostavnejših zgledih. Trideset točk v ravnini bi radi povezali z najkrajšo lomljeno črto. Matematiki pravijo temu problem trgovskega potnika. Ker je možnih poti-ciklov že pri več deset točkah ogromno, je problem zelo težek, celo tako težak, da se ga takrat ne rešuje točno. V našem primeru je možnih poti 29 fakulteta polovic ali približno 4 krat 10 na 30. Skratka preveč, da bi na silo pregledali vse možnosti. Obstajajo pa približne metode “optimiziranja kombinatoričnih problemov”, ki se točni rešitvi ali “globalnemu minimumu” zelo lepo približajo, kdaj ga kar zadenejo, drugič jim zmanjka kak odstotek. Slike spodaj od leve naprej: množica 30-ih točk, naključna pot (v izračunu dolga 32.4 enote) in najkrajša (8.8).

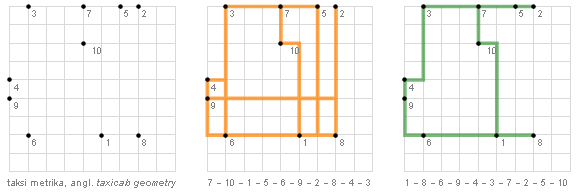
Točke v pravokotnem koordinatnem sistemu so šolski primer. Med seboj so oddaljene za “Evklidovo razdaljo”, ki jo izračunamo s Pitagorovim izrekom. Spodaj: so točke v kvadratni mreži, ki lahko predstavlja tloris mesta in ceste, po katerih vozi taksist. Kako narediti deset postankov po najkrajši poti? Enako kot zgoraj, drugačna je le “metrika” ali razdalja med točkami. In podobno je s točkami na zemljevidu: poznamo koordinate mest, poznamo polmer Zemlje in s tem izračunamo razdaljo med parom točk ali, kot smo že rekli, dolžino loka “velikega kroga”. Slike spodaj od leve naprej: označena postajališča v kvadratni mreži, naključna pot (v izračunu dolga 65 enot) in najkrajša (34).

Včeraj pred 136-imi leti je gospod Fogg s služabnikom Passepartoutom šel na pot okoli sveta, ker je stavil, da pride naokrog v 80-ih dneh. Knjigo smo brali in vemo, da mu je uspelo. (Pravzaprav izda to že naslov.) Takrat je bil to nedvomno podvig in tri četrt, danes pa se zdi pot rahlo dolgočasna.

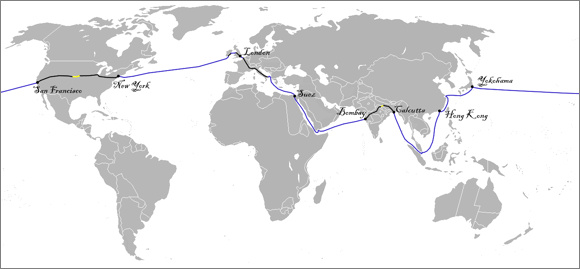
  Around the World in Eighty Days map - Wikipedia

Jules Verne ni povedal, kaj pomeni obkrožiti Zemljo. Iti okrog tečaja? Potem bi šli lahko naravnost na sever, meter do pola, naredili okoli šest metrski obhod in šli nazaj. In že obšli svet? No, mi smo natančno določili, kako naokrog: tako da smo obiskali vse države in v vsaki njeno glavno mesto. In če smo se med mesti premikali reaktivno s 700 km/h, nam je ostalo okoli 70 dni ali šest ur v vsakem mestu. Kar je, recimo, dovolj za temeljit študij svetovnih kavarn. Obudimo spomin in poglejmo pot še na globusu.